Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости, называется поверхностью вращения. Пусть некоторая кривая L лежит в плоскости Oyz. Уравнение этой кривой запишутся в виде:
Найдем уравнение поверхности, образованной вращением кривой L вокруг оси Oz.
Возьмем на поверхности точку
M (x;y;z). Проведем через точку
М плоскость, перпендикулярную
оси oz, и обозначим точки
пересечения ее с осью oz
и кривой L соответственно O 1 и N.
Обозначим координаты точки
N (0;y 1 ;z 1). Отрезки O 1 M и O 1 N
являются радиусами одной и той же окружности. Поэтому O 1 M = O 1 N. Но O 1 M = (x 2 +y 2) 0.5 , O 1 N=|y 1 |.
Следовательно, |y 1 |=(x 2 +y 2) 0.5 или y 1 =±(x 2 +y 2) 0.5 . Кроме того, очевидно, z 1 =z.
Следовательно – искомое уравнение поверхности вращения, ему удовлетворяют координаты любой точка М этой поверхности и не удовлетворяет координаты точек, не лежащих на поверхности вращения.
27. Поверхности 2-го порядка. Эллипсоид, Гиперболоид.
Эллипсоид.
Рассмотрим сечение поверхности с плоскостями, параллельными xOy. Уравнения таких плоскостей z=h, где h – любое число. Линия, получаемая в сечении, определяется двумя уравнениями:
Если |h|>c, c>0, то точек пересечения поверхности с плоскостямиz=h нет.
Если |h|=c, т.е. h=±c, то . Линия пересечения вырождается в две точки (0;0;с) и (0;0;-с). Плоскостиz=c и z=–c касаются поверхности.
Если
|h|
Линия пересечения есть эллипс с полуосями.
Эллипсоид – замкнутая овальная поверхность, где a,b,с – полуоси. Если все они различны, то эллипсоид называется трехосным . Если какие-либо две полуоси равны, то тело называется эллипсоид вращения, если a=b=c, то тело называется сферой x 2 +y 2 +z 2 =R 2
Однополостный гиперболоид.
Пересекая поверхность плоскостью z=h, получим линию пересечения, уравнения которой имеют вид.

Полуоси достигают своего наименьшего значения при h=0, a 1 =a, b 1 =b. При возрастании |h| полуоси будут увеличиваться.
Если пересекать поверхность плоскостями x=h или y=h, то в сечении получим гиперболы. Найдем линию пересечения поверхности с плоскостью Oyx, уравнение которой x=0. Эта линия пересечения описывается уравнениями:
Поверхность имеет форму бесконечно расширяющейся трубки и называется однополостным гиперболоидом .
Двуполостный гиперболоид.
Если поверхность пересечь плоскостями z=h, то линия пересечение уравнениями
Если
|h| Если
|h|=c,
то плоскости h=±c
касаются данной поверхности соответственно
в точках (0;0;с) и (0;0;-с). Если
|h|>c,
то уравнения можно переписать в виде:
Эти
уравнения определяют эллипс, полуоси
которого возрастают с ростом |h|. У
обеих гипербол действительной осью
является ось oz.
Метод сечения позволяет изобразить
поверхность, состоящую из двух полостей,
имеющих форму двух неограниченных чаш.
Поверхность называется двуполостным
гиперболоидом
. Эллиптический.
При
пересечении поверхности координатами
плоскостями Oxz
и Oyz
получается соответственно параболы
и.
Таким образом, поверхность, определяемая
уравнением, имеет вид выпуклой, бесконечно
расширяющейся чаши. Гиперболический.
Рассечем
поверхность плоскостями z=h.
Получим кривую которая
при всех h≠0
является гиперболой. При h>0
ее действительные оси параллельны оси
Ox,
при h<0
– параллельные оси Oy.
При h=0
линия пересечения распадается на пару
пересекающихся прямых: При
пересечении поверхности плоскостями,
параллельности плоскости Oxz
(y=h),
будут получаться параболы, ветви которых
направлены вверх. Скачать с Depositfiles Лекция № 12. Тема 6: Поверхности
6.1. Уравнение поверхности
Аналогично, как и для случая линии на плоскости, уравнение поверхности – это уравнение с тремя переменными , которому удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты никакой другой точки, не лежащей на поверхности. Верно и обратное, т.е.
каждое уравнение вида
вообще говоря, определяет некоторую поверхность в пространстве. Если уравнение (1) не удовлетворяется координатами ни одной точки, то говорят, что оно определяет мнимую поверхность. В дальнейшем такие случаи рассматривать не будем.
Пример 1.
Составить уравнение сферы радиуса
R
с центром в точке Пусть
которое и является искомым уравнением сферы.
Р задана некоторая линия, уравнение которой
М
1
полученной вращением этой линии вокруг
оси
O
z
.
N
Возьмём произвольную точку
O
у
этой поверхности и проведём плоскость,
перпендикулярную оси
O
y
. Очевидно, что
х
в сечении получим окружность с центром
в точке
N
. Тогда Аналогично можно получать уравнения поверхностей вращения относительно других координатных осей.
Пример 2.
Найти уравнение поверхности, образованной вращением эллипса Для этого случая нужно провести замену 6.2. Поверхности второго порядка
Пусть в некоторой ДСК задана поверхность, определяемая уравнением второй степени
где коэффициенты Рассмотрим частные случаи уравнения (2)
:
1.
Эллипсоид
. Его каноническое уравнение Чтобы составить представление об этой поверхности, проведём сечения плоскостями, параллельными координатным плоскостям. Предварительно заметим, что при замене уравнение эллипсоида не изменяется – это означает, что эта поверхность симметрична относительно координатных плоскостей. Например, пересекая эллипсоид плоскостями с z
c
a
b
b
y
a
x
c
Так же можно получить вид следующих поверхностей:
2 y
x
3.
Двуполостный гиперболоид
y
x
4.
Эллиптический параболоид
z
x
y
5.
Гиперболический параболоид
z
x
y
6.
Конус
y
x
7.
Эллиптический цилиндр
z
y
x
8.
Гиперболический цилиндр
9 y
x
10.
Пара пересекающихся плоскостей
.
Какие еще могут быть варианты взаимного расположения прямой с однополостным гиперболоидом?
Классификация кривых второго порядка.
Рассмотрим общее уравнение второго порядка (11.5): и выясним, какие геометрические образы на плоскости могут задаваться этим уравнением. 1. Если собственные числа матрицы А λ
1 и λ
2 одного знака, уравнение (11.5) называется уравнением эллиптического типа
. Его можно привести к виду (11.7): а) если имеет тот же знак, что и λ
1,2 , при делении на получаем Каноническое уравнение эллипса.
б) если =0, уравнение в) если знак противоположен знаку λ
1,2 , уравнение после деления на примет вид: 2. Если собственные числа матрицы А λ
1 и λ
2 разных знаков, уравнение (11.5) называется уравнением гиперболического типа
. а) при оно сводится к одному из двух видов: Или б) При =0 получаем уравнение , эквивалентное двум линейным уравнениям: и , задающим пару пересекающихся прямых
. 3. Если одно из собственных чисел равно 0, уравнение (11.5) называется уравнением параболического
типа, и его можно привести к одному из следующих видов: а) к уравнению (11.8): , определяющему параболу
; б) к уравнению , или , задающему пару параллельных прямых
; в) к уравнению , определяющему одну прямую
(или пару совпадающих прямых); г) к уравнению , не имеющему решений и, следовательно, не определяющему никакого геометрического образа. Определение 12.1.
Поверхностью второго порядка
называется множество точек трехмерного пространства, декартовы координаты которых удовлетворяют уравнению вида: уравнению второй степени от трех неизвестных, называемому общим уравнением поверхности второго порядка
. Если найти собственные числа и нормированные собственные векторы матрицы квадратичной формы и перейти к системе координат, определяемой базисом из ортонормированных собственных векторов, уравнение (12.1) можно привести к одному из следующих видов: 1. Если λ
1 , λ
2 , λ
3 – одного знака, уравнение (12.1) есть уравнение эллиптического типа и приводится к канонической форме: а) каноническое уравнение эллипсоида
. Замечание, Если два собственных числа совпадают, эллипсоид называется эллипсоидом вращения и представляет собой поверхность, полученную в результате вращения эллипса вокруг одной из его осей. Если все собственные числа равны, уравнение (12.2) становится уравнением сферы. б) уравнение задает точку в пространстве
; в) пустое множество. 2. Если собственные числа разных знаков, уравнение (12.1) приводится к каноническому виду: а) б) Каноническое уравнение двуполостного гиперболоида
, в) 
28. Поверхности 2-го порядка. Параболоиды.
 , (1)
, (1)
 .
.

текущая точка сферы, тогда для вектора
текущая точка сферы, тогда для вектора  с координатами должно выполняться условие
с координатами должно выполняться условие
 ассмотрим один из часто встречающихся случаев –
поверхности
вращения
. Пусть, например, в плоскости
O
yz
z
ассмотрим один из часто встречающихся случаев –
поверхности
вращения
. Пусть, например, в плоскости
O
yz
z
 . Найдём уравнение поверхности,
M
. Найдём уравнение поверхности,
M
 . С другой стороны, радиус этой окруж-ности
. С другой стороны, радиус этой окруж-ности  , где точка
М
1
принадлежит линии
.
Следовательно, для всех точек поверхности вращения должно выполняться уравнение
, где точка
М
1
принадлежит линии
.
Следовательно, для всех точек поверхности вращения должно выполняться уравнение

 в плоскости
O
xy
вокруг оси
O
x
.
в плоскости
O
xy
вокруг оси
O
x
.
 в уравнении эллипса. Тогда получим уравнение
в уравнении эллипса. Тогда получим уравнение  , которое определяет поверхность так называемого
эллипсоида вращения
.
, которое определяет поверхность так называемого
эллипсоида вращения
.
 одновременно не равны нулю. Эта поверхность называется поверхностью второго порядка.
одновременно не равны нулю. Эта поверхность называется поверхностью второго порядка.
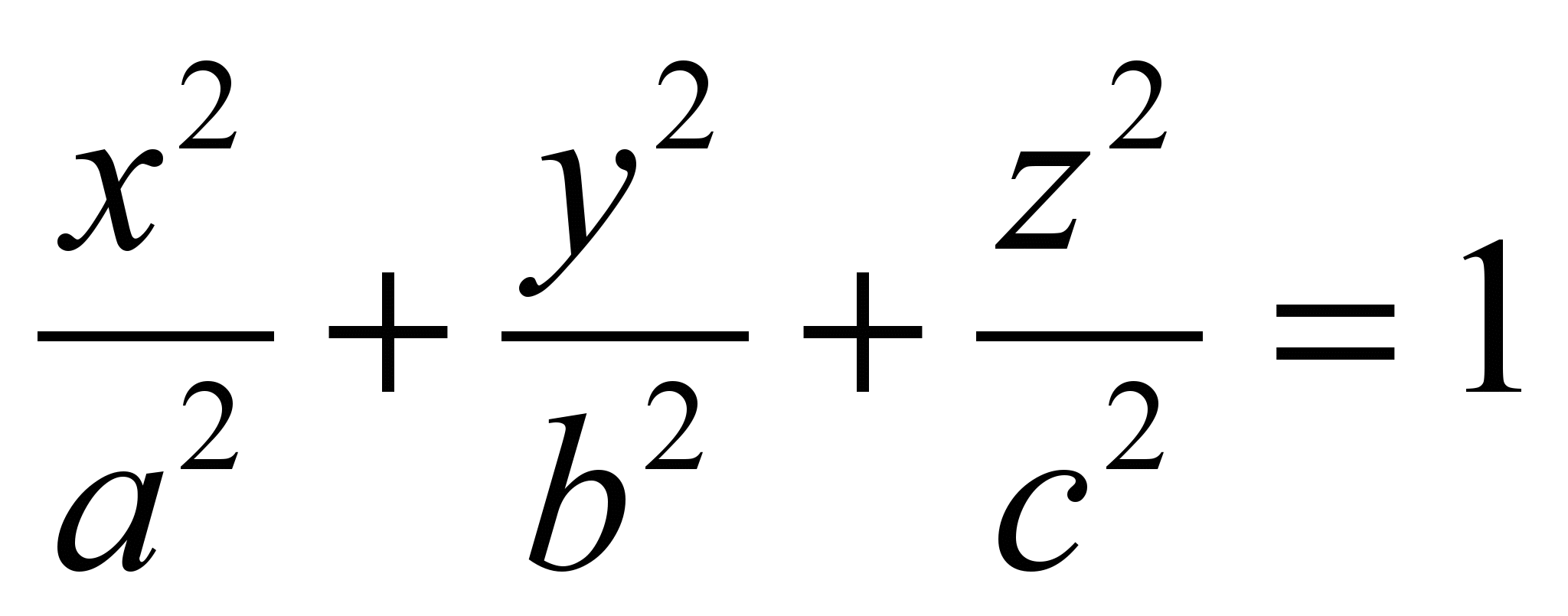 .
.
 , получаем в сечениях эллипсы вида
, получаем в сечениях эллипсы вида

 полуосями
полуосями  . Отсюда видно, что самый большой эллипс получается в сечении
. Отсюда видно, что самый большой эллипс получается в сечении
 а при увеличении
h
эллипсы уменьшаются, вырождаясь в точку при
а при увеличении
h
эллипсы уменьшаются, вырождаясь в точку при  . Аналогичная картина будет в сечениях плоскостями . На основании таких исследований можно определить вид эллипсоида.
. Аналогичная картина будет в сечениях плоскостями . На основании таких исследований можно определить вид эллипсоида.
 .
Однополостный гиперболоид
z
.
Однополостный гиперболоид
z


 z
z
 .
.

 .
.


 z
z



 .
Параболический цилиндр
z
.
Параболический цилиндр
z
 .
.
![]() , которое, в свою очередь, преобразуется в следующую форму:
, которое, в свою очередь, преобразуется в следующую форму:![]() имеет единственное решение: , определяющее точку на плоскости
.
имеет единственное решение: , определяющее точку на плоскости
.![]() . Множество его решений пусто (иногда это пустое множество называют мнимым эллипсом
).
. Множество его решений пусто (иногда это пустое множество называют мнимым эллипсом
).![]() , в зависимости от знака . Оба этих уравнения определяют гиперболу
.
, в зависимости от знака . Оба этих уравнения определяют гиперболу
.![]() - (12.2)
- (12.2)
![]() - (12.3)
- (12.3)![]() - (12.4)
- (12.4)![]() - каноническое уравнение однополостного гиперболоида,
(12.5)
- каноническое уравнение однополостного гиперболоида,
(12.5)
![]() - (12.6)
- (12.6)
![]() - (12.7)
- (12.7)



